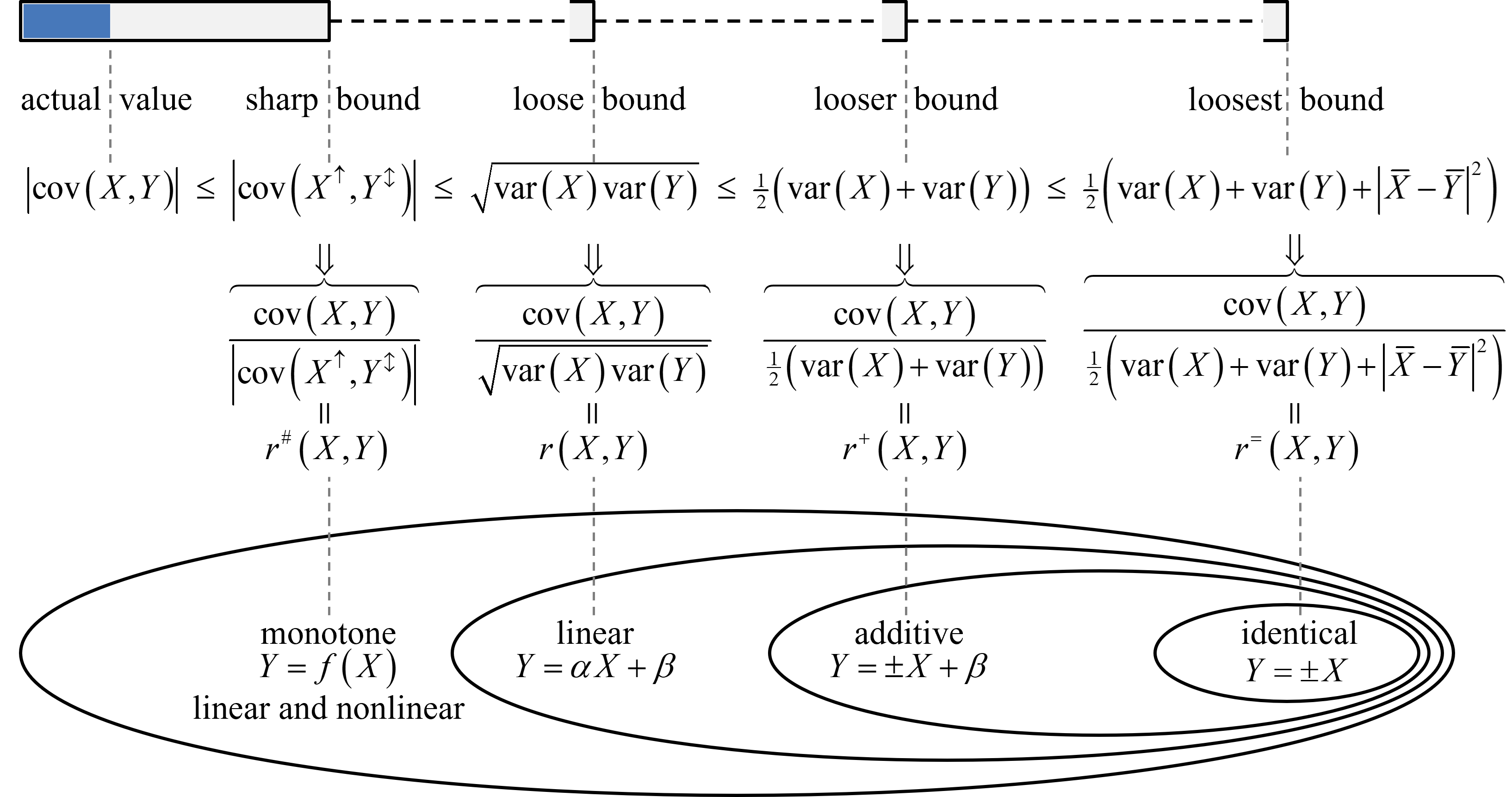
Journal:38th Conference on Neural Information Processing Systems (NeurIPS 2024；人工智能领域最负盛名的顶级学术会议之一；论文的相关报道）

Abstract:①为著名的Cauchy-Schwarz不等式找到了一个更加紧致的边界，得到了一个新的不等式系列；②基于新的不等式，对三大经典相关系数之一的Pearson相关系数进行了改进。改进之后的相关系数，可以度量包括线性关系（linear dependence）在内的任意单调依赖性（monotone dependence）。改进的相关系数，在线性情况下，将退化为Pearson相关系数；在秩上进行计算时，则退化为Spearman相关系数（同样为三大经典相关系数之一）；③该研究表明：现行大部分教材中关于Pearson相关系数的表述，“Pearson相关系数只能用来衡量线性关系”并不准确，更准确的表述可能是“线性关系可以完全被Pearson相关系数所衡量，任意单调依赖性可以在一定程度上被Pearson相关系数衡量”。

Note:相关报道网址： https://iea.bupt.edu.cn/info/1045/1245.htm

Indexed by:Unit Twenty Basic Research

First Author:Xinbo Ai

Translation or Not:no