高泽华，男，北京邮电大学博士，副教授, 研究生导师，2002年获得北京邮电大学博士学位，2002年于北京邮电大学信息与通信工程学院（原电信工程学院）任教。2015年-2016年在美国加州大学洛杉矶分校（UCLA）做访问学者。

       物联网与元宇宙创新实验室主任，北邮-海外创业平台负责人，国际TRIZ创新专家。北京邮电大学创业导师，启明星创新与创业平台创始人，北邮创业联盟发起人。中国电子学会高级会员、中国通信学会会员、北京通信信息协会会员。

       主要研究项目涉及：纳米机器人通信、元宇宙、6G体域网、物联网、太赫兹通信、人工智能感知技术、储能、创新方法TRIZ、交叉学科跨界科研等。主持承担了国家自然科学基金、国家863计划等多项项目，中国移动等运营商项目多项，在国际、国内学术期刊、会议发表一百余篇学术论文，主编及参加编写清华大学出版社出版《物联网——体系结构、协议标准与无线通信（RFID、NFC、LoRa、NB-IoT、WiFi、ZigBee与Bluetooth）》，《窄带物联网——NB-IoT原理、架构及应用》，《创新创业-数字化时代的创新思维与商业模式》，北京邮电大学出版社出版专著《物联网技术与创意》，科学出版社出版的《电磁场与电磁波》，电子工业出版社出版的《微波技术基础》等教材七部，主编及参编通信类书籍十九部。申请发明专利十九项，2008年第三届北京发明创新大赛获得金奖和通信信息类专项奖，2019所带北邮创业团队获得AIIA杯人工智能大赛全国总冠军。

        主讲现代通信技术，电磁场与电磁波，微波技术与天线，大学生创业，创新与创业-从硅谷到北邮等课程。

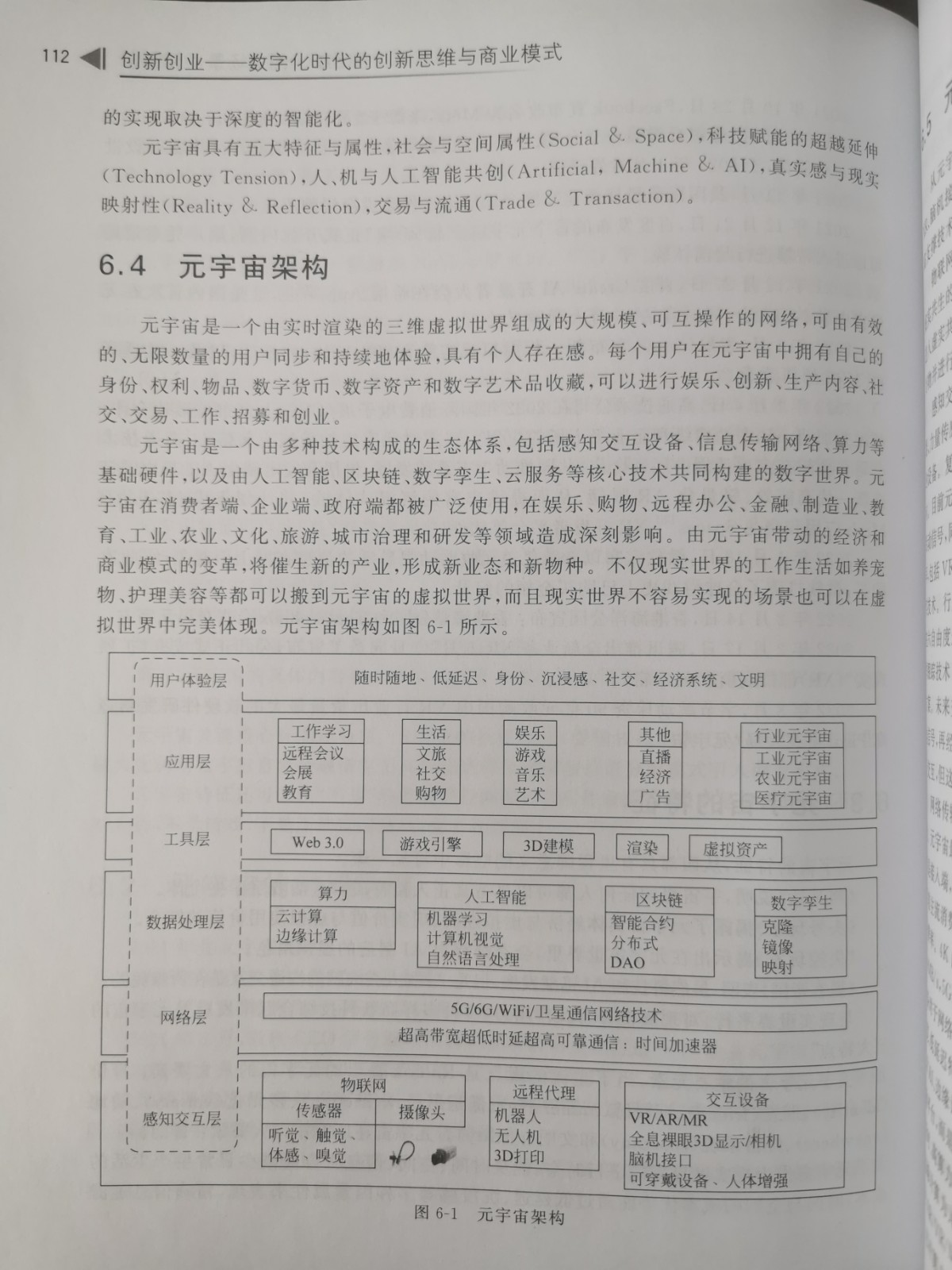
        教材 《创新创业-数字化时代的创新思维与商业模式》系统论述了创新思维、创新方法与创业路线，全面涵盖元宇宙、物联网、人工智能、大数据、区块链、自媒体、跨境电商等最新信息技术知识体系。

        提出一项具有颠覆性原创坐标系：支持计算机时代数字运算的区坐标系（Zehua Gao, et al. Zone Coordinates: A New Coordinate System. 2017 17th IEEE ICCT. 1774-1777），让科幻三体中的二向箔对太阳系二维展开时出现的bug。

        与海外创业孵化器合作在北京邮电大学创办创业平台，从海外引进创业资源涵盖硬核科技，颠覆性技术，互联网应用等，引入行业市场资源、第三方支付资源，以及网红、明星等流量资源、跨境物流资源，带领学生创业团队在创业资源基础上进行创业，提升创业层次和成功率。创业资源有：来自海外的颠覆性硬核技术：低功耗芯片技术、图像辨识大数据技术；物联网技术，AR增强现实技术，无人机，机器人，高性能电源及电机，汽车用氢燃料发电机，纳米材料（建筑、过滤、电池膜技术），水性防火漆，人工智能，区块链、驾驶元宇宙引擎、人体增强、脑机接口、数字孪生、富硒农业技术等技术。

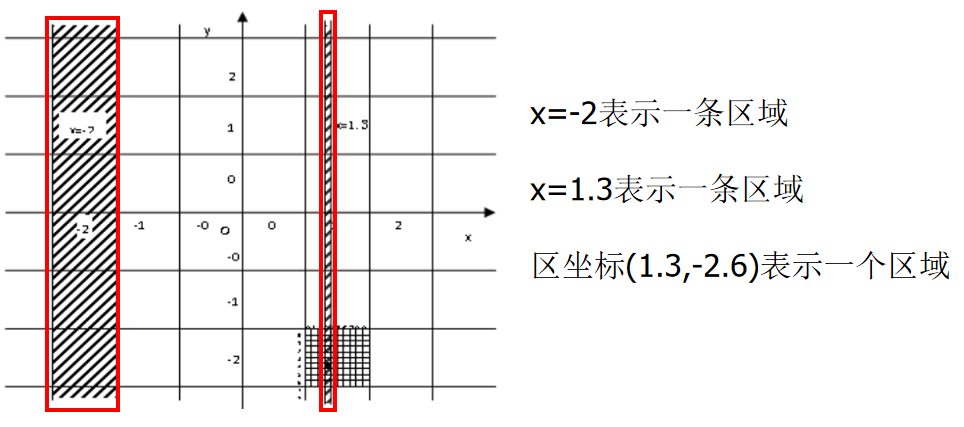
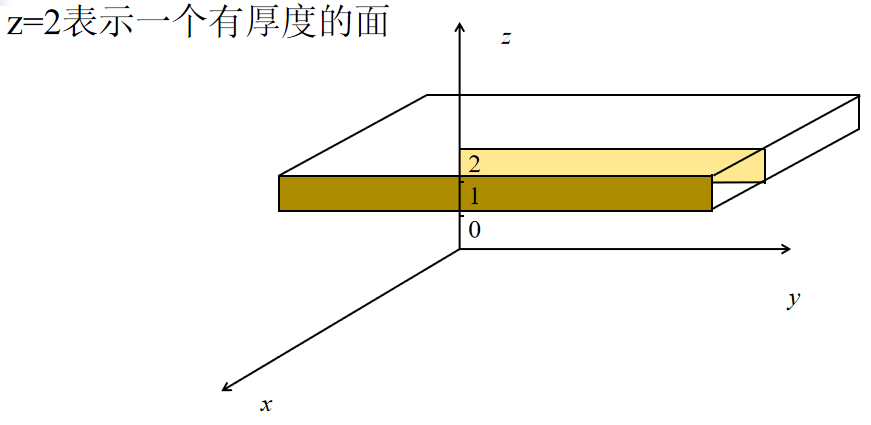
         颠覆性原创区坐标系介绍：科幻小说三体中第一梯队武器：二向箔，对太阳系二维展开后的面积是多少？无限大，这是很多人的第一判断，这是纯数学上的答案。但在物理上是不现实的，无限大将超过宇宙大爆炸产生的空间，这是数学上的bug。在物理上，厚度最小为普朗克长度1.6*10^(-35)m，可以得到太阳系二维展开后的面积是有限的，所以符合物理实际可实现的二维是有厚度的。物理理论基于数学，依赖数学，数学上的“面”在物理上竟然不存在。为了解决数学上的这个bug，基于物理实际，我们提出符合物理现实的区坐标系。在区坐标系中，线是有宽度的，面是有厚度的，点是有半径的，完全颠覆传统坐标系点线面的横向尺寸为0的定义。

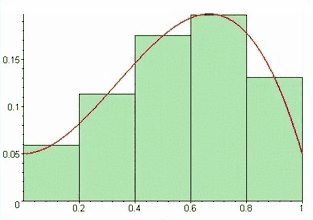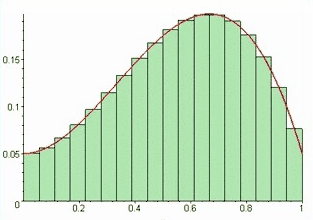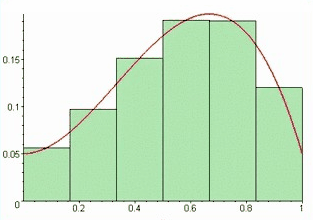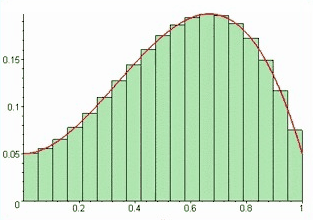
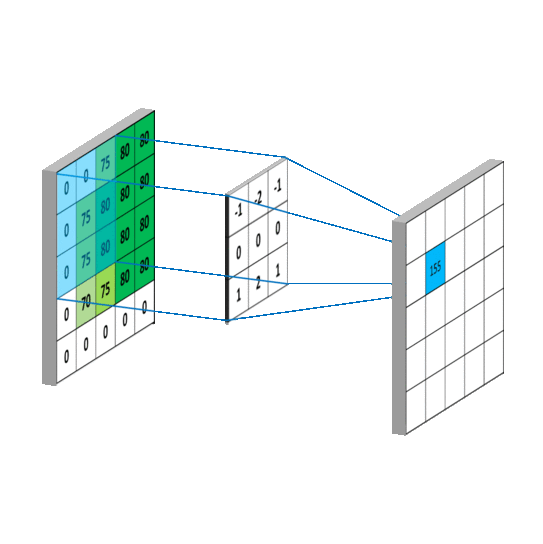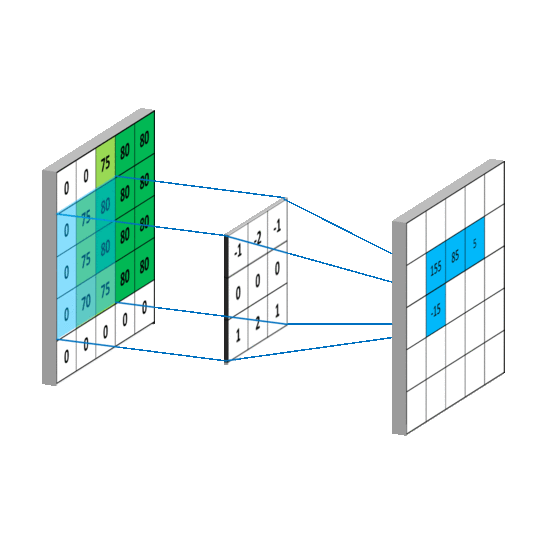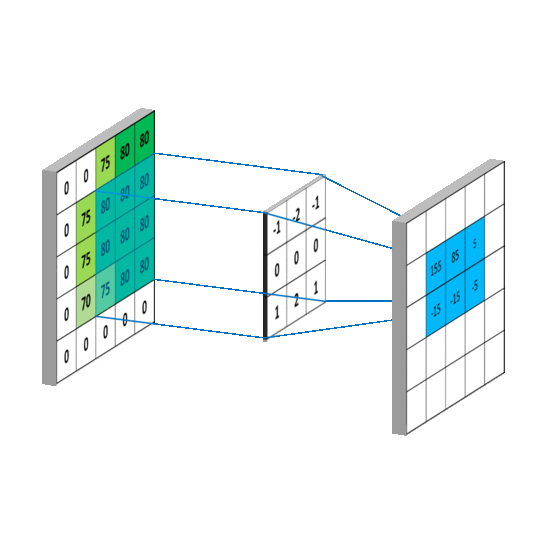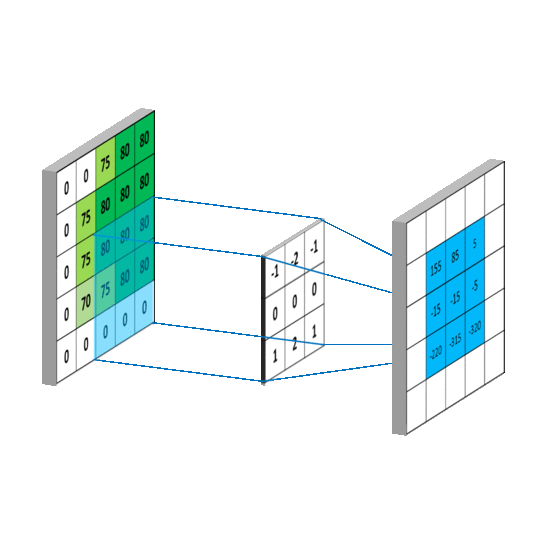
         在现实世界中即使小到原子、中子质子，都是占有一定空间尺寸。在计算机数字信息处理中每个存储的bit都占有一定空间，都是数字化的，区坐标系是特别适合物理现实的坐标系，在计算机、数学运算如矩阵运算都可以运用区坐标系去实现，区坐标系把数字运算放到几何空间中实现。如定积分（第一步分割就可以省略）、离散傅里叶变换，数字卷积运算都可以基于区坐标系去运算。在物理定位上将带来极大的方便性。

         工业革命时代以微积分为代表的连续数学占主流的地位，随着信息时代的到来，离散数学越来越重要。离散数学的思想广泛地体现在计算机科学技术及相关专业的诸领域，数字电子计算机是一个离散结构，它只能处理离散的或离散化了的数量关系。离散数学是逻辑学，集合论（包括函数），数论基础，算法设计，组合分析，离散概率，关系理论，图论与树，抽象代数（包括代数系统，群、环、域等），布尔代数，计算模型（语言与自动机）等汇集起来的一门综合学科。离散数学是计算机科学的基础核心学科。传统坐标系是为连续数学、连续函数准备的。离散函数、离散数字运算如离散傅里叶变换，矩阵运算没坐标系可以用。我们提出的区坐标系是为离散数学使用的。

        从逻辑层面来看，根本没有办法证明连续性假设。自牛顿以来，人们都是用分析学的眼光看世界，用连续流形、连续场来描写物理现象，特别是爱因斯坦的广义相对论亦是如此 。之后以几何的眼光看世界成为物理的主流。在这个思路下，物理学家发展了规范场论、量子场论，以及描写所有基本粒子的标准模型。从量子革命以来人们越来越意识到，世界不是连续的，而是离散的，应该用代数学的眼光看世界。就像连续的流体，是许许多多一个个分子集体运动的表象。以代数的眼光看世界的新思想，颠覆很多主流物理理论，带来物理的第二次量子革命 。第一次量子革命的数学基础是线性代数。近100 来近代数学发展就是一条从连续到离散、从分析到代数的脉络，离散的代数比连续的分析更本质。

        区坐标系可以用在：离散数学（离散数学汇集了逻辑学，集合论（包括函数），数论基础，算法设计，组合分析，离散概率，分形迭代，混沌，矩阵运算，关系理论，图论与树，抽象代数（包括代数系统，群、环、域等），布尔代数，计算模型（语言与自动机）等）、序列几何、离散几何、积分、地理测绘、测量、度量、误差、公差分析、加工余量、矩阵量子力学、量子力学中的“不确定原理”、模拟信号数字化中抽样量化编码中的量化、Smith Chart、衍射光栅、干涉条纹、窗口参数、生命科学中的生命窗口参数、实验数据统计分析曲线拟合、点阵、艺术设计、雕刻，以及位置相关应用等等。位置相关应用如地理坐标定位、GPS定位、导弹定位、武器瞄准、建筑位置、地铁等交通工具停车位置、电梯位置、材料检测定位区域分布、缺陷分布区域分布、硬盘存储位置等等。